
最后编辑于: 2021-11-08 15:22 | 分类: 算法&技术思想 | 标签: 字符串 | 浏览数: 1805 | 评论数: 0
Original address:http://blog.csdn.net/sealyao/article/details/4568167#
在用于查找子字符串的算法当中,BM(Boyer-Moore) 算法是目前相当有效又容易理解的一种,一般情况下,比KMP算法快3-5倍。
BM算法在移动模式串的时候是从左到右,而进行比较的时候是从右到左的。
常规的匹配算法移动模式串的时候是从左到右,而进行比较的时候也是是从左到右的,基本框架是:
j = 0;
while(j <= strlen(主串)- strlen(模式串)){
for (i = 0;i < strlen(模式串) && 模式串[i] == 主串[i + j]; ++i);
if (i == strlen(模式串))
Match;
else
++j;
} 而BM算法在移动模式串的时候是从左到右,而进行比较的时候是从右到左的,基本框架是:
j = 0;
while (j <= strlen(主串) - strlen(模式串)) {
for (i = strlen(模式串) - 1; i >= 0 && 模式串[i] ==主串[i + j]; --i)
if (i < 0)
match;
else
++j;
} 显然BM算法并不是上面那个样子,BM算法的精华就在于++j
BM算法实际上包含两个并行的算法,坏字符算法和好后缀算法。这两种算法的目的就是让模式串每次向右移动尽可能大的距离(j+=x,x尽可能的大)。
几个定义:
例主串和模式串如下:
主串: mahtavaatalomaisema omalomailuun
模式串: maisemaomaloma
好后缀:模式串中的aloma为“好后缀”。
坏字符:主串中的“t”为坏字符。
如果程序匹配了一个好后缀, 并且在模式中还有另外一个相同的后缀, 那把下一个后缀移动到当前后缀位置。
好后缀算法有两种情况:
Case1:模式串中有子串和好后缀安全匹配,则将最靠右的那个子串移动到好后缀的位置。继续进行匹配。

Case2:如果不存在和好后缀完全匹配的子串,则在好后缀中找到具有如下特征的最长子串,使得P[m-s…m]=P[0…s]。说不清楚的看图。
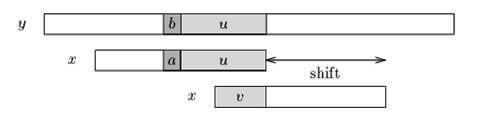
当出现一个坏字符时, BM算法向右移动模式串, 让模式串中最靠右的对应字符与坏字符相对,然后继续匹配。
坏字符算法也有两种情况。
Case1:模式串中有对应的坏字符时,见图。

Case2:模式串中不存在坏字符。见图。
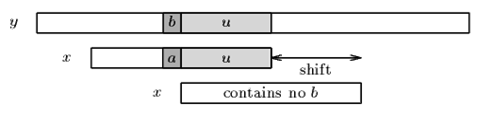
BM算法的移动规则是:
将概述中的++j,换成j+=MAX(shift(好后缀),shift(坏字符)),即
BM算法是每次向右移动模式串的距离是,按照好后缀算法和坏字符算法计算得到的最大值。
shift(好后缀)和shift(坏字符)通过模式串的预处理数组的简单计算得到。
好后缀算法的预处理数组是bmGs[],坏字符算法的预处理数组是BmBc[]。
BM算法子串比较失配时,按坏字符算法计算模式串需要向右移动的距离,要借助BmBc数组。
注意BmBc数组的下标是字符,而不是数字。
BmBc数组的定义,分两种情况。

BM算法子串比较失配时,按好后缀算法计算模式串需要向右移动的距离,要借助BmGs数组。
BmGs数组的下标是数字,表示字符在模式串中位置。
BmGs数组的定义,分三种情况。



在计算BmGc数组时,为提高效率,先计算辅助数组Suff。
Suff数组的定义:suff[i] = 以i为边界, 与模式串后缀匹配的最大长度,即P[i-s…i]=P[m-s…m]如下图:

举例如下:
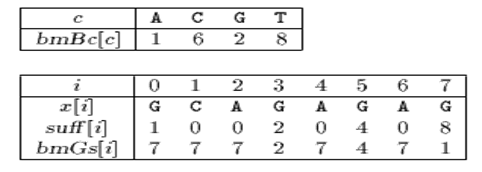
用Suff[]计算BmGs的方法。
for(i=0;i
if(-1==i || Suff[i] == i+1)
for(;j < m-1-i;++j)
if(suff[j] == m)
BmGs[j] = m-1-i;
for(i=0;i
BmGs[m-1-suff[i]] = m-1-i;
如下图所示:

Suff[]数组的计算方法。
常规的方法:如下,很裸很暴力。
Suff[m-1]=m;
for(i=m-2;i>=0;--i){
q=i;
while(q>=0&&P[q]==P[m-1-i+q])
--q;
Suff[i]=i-q;
}
有聪明人想出一种方法,对常规方法进行改进。基本的扫描都是从右向左。改进的地方就是利用了已经计算得到的suff[]值,计算现在正在计算的suff[]值。
如下图所示:
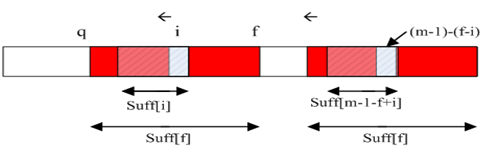
i是当前正准备计算的suff[]值得那个位置。
f是上一个成功进行匹配的起始位置(不是每个位置都能进行成功匹配的,实际上能够进行成功匹配的位置并不多)。
q是上一次进行成功匹配的失配位置。
如果i在q和f之间,那么一定有P[i]=P[m-1-f+i];并且如果suff[m-1-f+i]=i-q, suff[i]和suff[m-1-f+i]就没有直接关系了。
void preBmBc(char *x, int m, int bmBc[]) {
int i;
for (i = 0; i < ASIZE; ++i)
bmBc[i] = m;
for (i = 0; i < m - 1; ++i)
bmBc[x[i]] = m - i - 1;
}
void suffixes(char *x, int m, int *suff) {
int f, g, i;
f = 0;
suff[m - 1] = m;
g = m - 1;
for (i = m - 2; i >= 0; --i) {
if (i > g && suff[i + m - 1 - f] < i - g)
suff[i] = suff[i + m - 1 - f];
else {
if (i < g)
g = i;
f = i;
while (g >= 0 && x[g] == x[g + m - 1 - f])
--g;
suff[i] = f - g;
}
}
}
void preBmGs(char *x, int m, int bmGs[]) {
int i, j, suff[XSIZE];
suffixes(x, m, suff);
for (i = 0; i < m; ++i)
bmGs[i] = m;
j = 0;
for (i = m - 1; i >= 0; --i)
if (suff[i] == i + 1)
for (; j < m - 1 - i; ++j)
if (bmGs[j] == m)
bmGs[j] = m - 1 - i;
for (i = 0; i <= m - 2; ++i)
bmGs[m - 1 - suff[i]] = m - 1 - i;
}
void BM(char *x, int m, char *y, int n) {
int i, j, bmGs[XSIZE], bmBc[ASIZE];
/* Preprocessing */
preBmGs(x, m, bmGs);
preBmBc(x, m, bmBc);
/* Searching */
j = 0;
while (j <= n - m) {
for (i = m - 1; i >= 0 && x[i] == y[i + j]; --i);
if (i < 0) {
OUTPUT(j);
j += bmGs[0];
}
else
j += MAX(bmGs[i], bmBc[y[i + j]] - m + 1 + i);
}
} 再附上一个BM算法的E文wiki条目里的code:
http://en.wikipedia.org/wiki/Boyer%E2%80%93Moore_string_search_algorithm
#include <stdint.h>
#include <stdlib.h>
#define ALPHABET_LEN 255
#define NOT_FOUND patlen
#define max(a, b) ((a < b) ? b : a)
// delta1 table: delta1[c] contains the distance between the last
// character of pat and the rightmost occurence of c in pat.
// If c does not occur in pat, then delta1[c] = patlen.
// If c is at string[i] and c != pat[patlen-1], we can
// safely shift i over by delta1[c], which is the minimum distance
// needed to shift pat forward to get string[i] lined up
// with some character in pat.
// this algorithm runs in alphabet_len+patlen time.
void make_delta1(int *delta1, uint8_t *pat, int32_t patlen) {
int i;
for (i=0; i < ALPHABET_LEN; i++) {
delta1[i] = NOT_FOUND;
}
for (i=0; i < patlen-1; i++) {
delta1[pat[i]] = patlen-1 - i;
}
}
// true if the suffix of word starting from word[pos] is a prefix
// of word
int is_prefix(uint8_t *word, int wordlen, int pos) {
int i;
int suffixlen = wordlen - pos;
*// could also use the strncmp() library function here*
for (i = 0; i < suffixlen; i++) {
if (word[i] != word[pos+i]) {
return 0;
}
}
return 1;
}
// length of the longest suffix of word ending on word[pos].
// suffix_length("dddbcabc", 8, 4) = 2
int suffix_length(uint8_t *word, int wordlen, int pos) {
int i;
// increment suffix length i to the first mismatch or beginning*
// of the word*
for (i = 0; (word[pos-i] == word[wordlen-1-i]) && (i < pos); i++);
return i;
}
// delta2 table: given a mismatch at pat[pos], we want to align
// with the next possible full match could be based on what we
// know about pat[pos+1] to pat[patlen-1].
//
// In case 1:
// pat[pos+1] to pat[patlen-1] does not occur elsewhere in pat,
// the next plausible match starts at or after the mismatch.
// If, within the substring pat[pos+1 .. patlen0], lies a prefix
// of pat, the next plausible match is here (if there are multiple
// prefixes in the substring, pick the longest). Otherwise, the
// next plausible match starts past the character aligned with*
// pat[patlen-1].
//
// In case 2:
// pat[pos+1] to pat[patlen-1] does occur elsewhere in pat. The
// mismatch tells us that we are not looking at the end of a match.
// We may, however, be looking at the middle of a match.
//
// The first loop, which takes care of case 1, is analogous to
// the KMP table, adapted for a 'backwards' scan order with the
// additional restriction that the substrings it considers as*
// potential prefixes are all suffixes. In the worst case scenario
// pat consists of the same letter repeated, so every suffix is
// a prefix. This loop alone is not sufficient, however:
// Suppose that pat is "ABYXCDEYX", and text is ".....ABYXCDEYX".
// We will match X, Y, and find B != E. There is no prefix of pat
// in the suffix "YX", so the first loop tells us to skip forward
// by 9 characters.
// Although superficially similar to the KMP table, the KMP table
// relies on information about the beginning of the partial match
// that the BM algorithm does not have.
//
// The second loop addresses case 2. Since suffix_length may not be
// unique, we want to take the minimum value, which will tell us
// how far away the closest potential match is.
void make_delta2(int *delta2, uint8_t *pat, int32_t patlen) {
int p;
int last_prefix_index = patlen-1;
// first loop
for (p=patlen-1; p>=0; p--) {
if (is_prefix(pat, patlen, p+1)) {
last_prefix_index = p+1;
}
delta2[p] = last_prefix_index + (patlen-1 - p);
}
// second loop
for (p=0; p < patlen-1; p++) {
int slen = suffix_length(pat, patlen, p);
if (pat[p - slen] != pat[patlen-1 - slen]) {
delta2[patlen-1 - slen] = patlen-1 - p + slen;
}
}
}
uint8_t* boyer_moore (uint8_t *string, uint32_t stringlen, uint8_t *pat, uint32_t patlen) {
int i;
int delta1[ALPHABET_LEN];
int *delta2 = malloc(patlen * sizeof(int));
make_delta1(delta1, pat, patlen);
make_delta2(delta2, pat, patlen);
i = patlen-1;
while (i < stringlen) {
int j = patlen-1;
while (j >= 0 && (string[i] == pat[j])) {
--i;
--j;
}
if (j < 0) {
free(delta2);
return (string + i+1);
}
i += max(delta1[string[i]], delta2[j]);
}
free(delta2);
return NULL;
}