
最后编辑于: 2010-09-14 12:59 | 分类: 算法&技术思想 | 标签: | 浏览数: 2605 | 评论数: 0
亚历山大港的丢番图(希腊语:Δι?φαντο? ? ?λεξανδρε??,生卒年约公元前200~214至公元前284~298),有“代数之父”之称;也有人认为此称谓应与比他大约晚出生五百年的一位波斯数学家花拉子米共享。丢番图是古希腊亚历山大港的数学家,他作著的丛书《算术》(Arithmetica)处理求解代数方程组的问题,但其中有不少已经遗失。后来当法国数学家费马(Pierre de Fermat)研究《算术》一书时,对其中某个方程颇感兴趣并认为其无解,说他对此“已找到一个绝妙的证明”,但他却没有写下来,三个世纪后才出现完整的证明,详见费马大定理。在数论中常常能看到他的名字,如丢番图方程、丢番图几何、丢番图逼近等都是数学里重要的研究领域。丢番图是第一个承认分数是一种数的希腊数学家--他允许方程中的系数和解为有理数,这是在数学史中具有开创性的。不过在今天,丢番图方程一词通常指以整数作为系数的代数方程,而其解也要求是整数。丢番图在数学符号方面也作出了贡献。
丢番图方程又名不定方程、整系数多项式方程,是变量仅容许是整数的多项式等式;即形式如
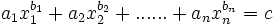
中所有的 aj、bj 和 c 均是整数,若其中能找到一组整数解 m1, m2 … mn 者则称之有整数解。
丢番图问题有数条等式,其数目比未知数的数目少;丢番图问题要求找出对所有等式都成立的整数组合。对丢番图问题的数学研究称为丢番图分析。
3世纪希腊数学家亚历山大城的丢番图曾对这些方程进行研究。
丢番图方程的例子有贝祖等式、勾股定理的整数解、四平方和定理和费马最后定理等。
代数之父——丢番图(Diophantine)是一位古希腊的大数学家,为第一位懂得使用符号代表数来研究问题的人。
其中丢番图最著名的可能就是他的墓志铭了: “坟中安葬著丢番图,多么令人惊讶,它忠实地记录了所经历的道路。 上帝给予的童年占六分之一,又过十二分之一,两颊长胡,再过七分之一,点燃起结婚的蜡烛。 五年之后天赐贵子,可怜迟到的宁馨儿,享年仅及其父之半,便进入冰冷的墓。 悲伤只有用数论的研究去弥补,又过四年,他也走完了人生的旅途。” 我们可以从中知道:“丢番图的一生,幼年占1/6,青少年占1/12,又过了1/7才结婚,5年后生子,子先父4年而卒,寿为其父之半。” 计算丢番图的方程为X/6 + X/12 + X/7 + 5 + X/2 + 4 = X,X = 84,由此知道丢番图享年84岁。
一次不定方程是形式如 a1x1 + a2x2 + … + anxn = c 的方程,一次不定方程有整数解的充要条件为: (a1, …, an) 须是c的因子,其中 (a1, …, an) 表示 a1, …, an 的最大公因子。
若有二元一次不定方程 ax + by = c,且 (a,b) | c,则其必有一组整数解 x1, y1,并且还有以下关系式:
t 为任意整数,故此一次不定方程有无限多解。请参见贝祖等式。
1900年,希尔伯特提出丢番图问题的可解答性为他的23个问题中的第10题。1970年,一个数理逻辑的结果马蒂雅谢维奇定理(Matiyasevich's theorem)说明:一般来说,丢番图问题都是不可解的。更精确的说法是,不可能存在一个算法能够判定任何丢番图方程式否有解,甚至,在任何相容于皮亚诺算数的系统当中,都能具体构造出一个丢番图方程,使得没有任何办法可以判断它是否有解。