最后编辑于: 2008-09-10 10:41 | 分类: 算法&技术思想 | 标签: 图像处理 | 浏览数: 1806 | 评论数: 0
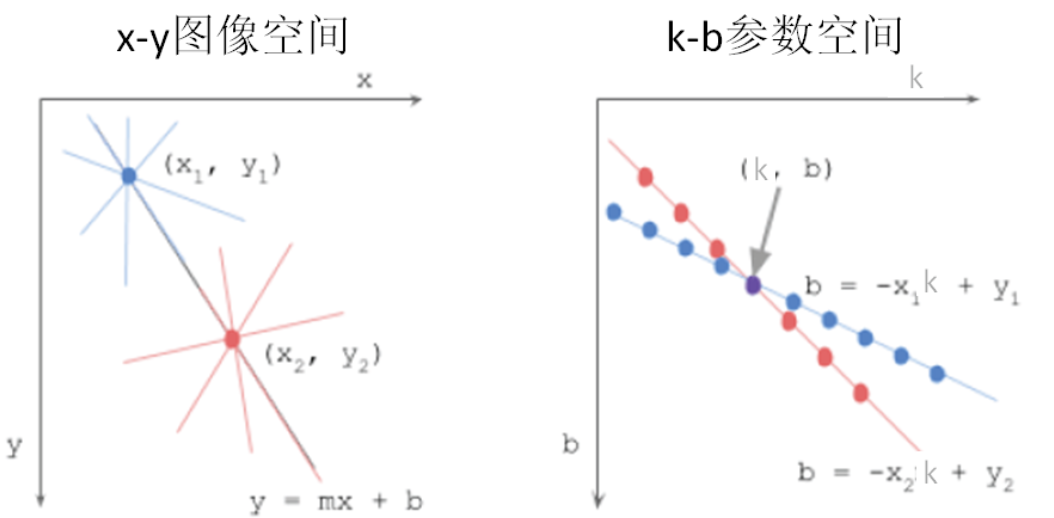
直线的方程可以用 y=k*x+b 来表示,其中k和b是参数,分别是斜率和截距。
过 某一点(x0, y0) 的所有直线的参数都会满足方程y0=kx0+b。
即点(x0,y0)确定了一族直线。方程y0=kx0+b在参数k--b平面上是一条直线。
这样,图像x--y平面上的一个前景像素点就对应到参数平面上的一条直线。
举个例子说明解决前面那个问题的原理。
设图像上的直线是y=x, 我们先取上面的三个点:A(0,0), B(1,1), C(22)。
可以求出,过A点的直线的参数要满足方程b=0, 过B点的直线的参数要满足方程1=k+b, 过C点的直线的参数要满足方程2=2k+b, 这三个方程就对应着参数平面上的三条直线,而这三条直线会相交于一点(k=1,b=0)。
同理,原图像上直线y=x上的其它点(如(3,3),(4,4)等)对应参数平面上的直线也会通过点(k=1,b=0)。
这个性质就为解决问题提供了方法:
首先,初始化一块缓冲区,对应于参数平面,将其所有数据置为0. 对于图像上每一前景点,求出参数平面对应的直线,把这直线上的所有点的值都加1。最后,找到参数平面上最大点的位置,这个位置就是原图像上直线的参数。
上面就是霍夫变换的基本思想。就是把图像平面上的点对应到参数平面上的线,最后通过统计特性来解决问题。假如图像平面上有两条直线,那么最终在参数平面上就会看到两个峰值点,依此类推。
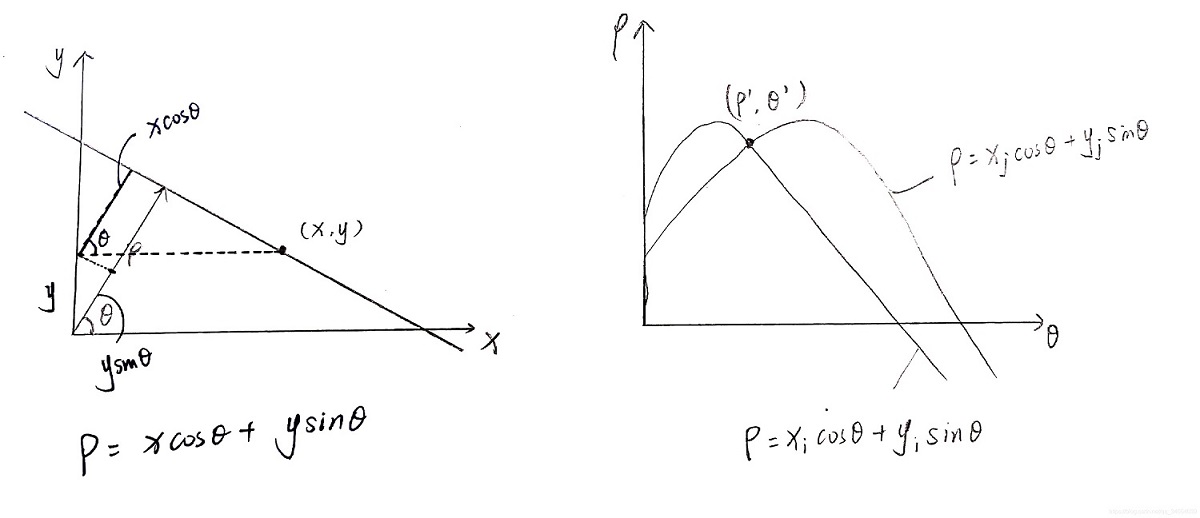
在实际应用中,y=k*x+b形式的直线方程没有办法表示x=c形式的直线 (这时候,直线的斜率为无穷大)。所以实际应用中,是采用参数方程p=x*cos(theta)+y*sin(theta)。这样,图像平面上的一个点就对应到参数p---theta平面上的一条曲线上。其它的还是一样。