
最后编辑于: 2021-07-24 23:31 | 分类: 算法&技术思想 | 标签: 图像处理 matlab | 浏览数: 2341 | 评论数: 0
% 数字图像处理程序作业
% 本程序能将JPG格式的彩色图像文件灰度化并进行直方图均衡
%
% 输入文件:PicSample.jpg 待处理图像
% 输出文件:PicSampleGray.bmp 灰度化后图像
% PicEqual.bmp 均衡化后图像
%
% 输出图形窗口说明
% figure NO 1 待处理彩色图像
% figure NO 2 灰度化后图像
% figure NO 3 直方图
% figure NO 4 均衡化后直方图
% figure NO 5 灰度变化曲线
% figure NO 6 均衡化后图像
% 1, 处理的图片名字要为 PicSample.jpg
% 2, 程序每次运行时会先清空workspace
% 作者: archiless lorder
clear all
%一,图像的预处理,读入彩色图像将其灰度化
PS=imread('PicSample.jpg'); %读入JPG彩色图像文件
imshow(PS) %显示出来 figure NO1
title('输入的彩色JPG图像')
imwrite(rgb2gray(PS),'PicSampleGray.bmp'); %将彩色图片灰度化并保存
PS=rgb2gray(PS); %灰度化后的数据存入数组
figure,imshow(PS) %显示灰度化后的图像,也是均衡化前的样品figure NO 2
title('灰度化后的图像')
%二,绘制直方图
[m,n]=size(PS); %测量图像尺寸参数
GP=zeros(1,256); %预创建存放灰度出现概率的向量
for k=0:255
GP(k+1)=length(find(PS==k))/(m*n); %计算每级灰度出现的概率,将其存入GP中相应位置
end
figure,bar(0:255,GP,'g') %绘制直方图 figure NO 3
title('原图像直方图')
xlabel('灰度值')
ylabel('出现概率')
%三,直方图均衡化
S1=zeros(1,256);
for i=1:256
for j=1:i
S1(i)=GP(j)+S1(i); %计算Sk
end
end
S2=round(S1*256); %将Sk归到相近级的灰度
for i=1:256
GPeq(i)=sum(GP(find(S2==i))); %计算现有每个灰度级出现的概率
end
figure,bar(0:255,GPeq,'b') %显示均衡化后的直方图 figure NO 4
title('均衡化后的直方图')
xlabel('灰度值')
ylabel('出现概率')
figure,plot(0:255,S2,'r') %显示灰度变化曲线 figure NO 5
legend('灰度变化曲线')
xlabel('原图像灰度级')
ylabel('均衡化后灰度级')
%四,图像均衡化
PA=PS;
for i=0:255
PA(find(PS==i))=S2(i+1); %将各个像素归一化后的灰度值赋给这个像素
end
figure,imshow(PA) %显示均衡化后的图像 figure NO 6
title('均衡化后图像')
imwrite(PA,'PicEqual.bmp');function erode0207all(Input,thresh,element)
% 本程序能够对灰度图像先进行二值化,再进行腐蚀操作
% 格式介绍: Input为欲处理的灰度图像;
% thresh为自选的阈值参数进行二值化,可输入0到255之间任意整数
% element为进行腐蚀操作的结构单元,本程序可提供3×3、5×5、7×7等奇数方阵的结构单元,原点都在中心位置,建议用三阶或五阶方阵
% 作者: archiless lorder
%----------------------------Begin Code------------------------------
% 一,图像二值化处理
[m,n]=size(Input); % 确定原图像的长、宽
Two=zeros(m,n); % 定义二值化矩阵
Two(find(Input>=thresh))=1; % 对原图像进行二值化处理
% 二,腐蚀操作前的预处理
Temp=zeros(element); % 定义3×3或5×5的结构单元
Output=zeros(m,n); % 定义输出矩阵
s=m+1-element; % s、t为循环长度
t=n+1-element;
Length=element-1; % Length和Radius的含义在循环中介绍
Radius=Length/2;
square=element*element; % 两个结构单元中元素的总和,即 9 、25 、49…………
% 三,进行腐蚀操作
for i=1:s
for j=1:t
Temp=Two(i:i+Length,j:j+Length); % 从二值化图像中依次取出三阶或五阶方阵
if sum(Temp(:))==square % 判断方阵中元素总和为 9 或 25 时
Output(i+Radius,j+Radius)=1; %方阵中心元素在输出矩阵中相应位置上的值为1
end
end
end
% 四,输出处理前后的图像
figure,subplot(221),imshow(Input),title('原图像');
subplot(222),imshow(Two),title('二值化后的图像');
subplot(223),imshow(Output),title('腐蚀后的图像');
%--------------------------------End Code--------------------------------function PicOut=Lap_edge(PicInput,thresh)
% 本程序能够将BMP格式的黑白灰度图像用拉普拉斯算子进行边缘检测
% 生物图像处理作业2
% 格式为 a=Lap_edge(PicInput,thresh) 或者嵌套为 Lap_edge(imread('rice.tif'),15)
% thresh参数可自选,对于rice.tif这张图来说最合适的值大约为14到18
% 使用例子:PicInput=imread('rice.tif');
% a=Lap_edge(PicInput,15);
% 作者: archiless lorder
%---------------- BEGIN CODE ----------------
% 一,原图像预处理,读入黑白图片并确定长和宽
[m,n]=size(PicInput); %确定图片的长和宽
% 二,拉普拉斯变换预处理,定义镜框矩阵和输出矩阵
r=m+2; %把图片的长和宽各加2
c=n+2;
PicFrame=zeros(r,c); %定义二维数组"PicFrame",长、宽比"Input"各多2,成为镜框的尺寸
b=zeros(m,n); %定义滤波后的数组
% 三,拉普拉斯运算的三个矩阵
Temp=zeros(3); %定义三阶方阵"Temp",为临时矩阵
op=[0 -1 0;-1 4 -1;0 -1 0]; %定义拉普拉斯算子
Result=zeros(3); %定义三阶方阵"Result",为运算结果矩阵
% 四,原图像矩阵处理,做一个"像框"
PicFrame(2:m+1,2:n+1)=PicInput; %把原图的矩阵放到新的矩阵"PicFrame"中心,它的第一行、最后一行、第一列、
%最后一列都是"0",即原图矩阵周围有一圈"0"的边缘,好像给图像加一个像框
PicFrame(1,:)=PicFrame(2,:); %把第二行的值赋给第一行
PicFrame(r,:)=PicFrame(r-1,:); %把倒数第二行的值赋给最后一行
PicFrame(:,1)=PicFrame(:,2); %把第二列的值赋给第一列
PicFrame(:,c)=PicFrame(:,c-1); %把倒数第二列的值赋给最后一列
% 五,用拉普拉斯算子进行滤波
for i=1:m
for j=1:n
Temp=PicFrame(i:i+2,j:j+2); %从"PicFrame"矩阵中依次取出三阶方阵,赋值给临时矩阵"Temp"
Result=Temp.*op; %临时矩阵与拉普拉斯算子"点乘",赋值给结果矩阵"Result"
b(i,j)=sum(sum(Result));
%结果矩阵中"十"字线上元素相加,赋值给输出矩阵中相应的位置,
%即临时矩阵中心元素所对应的位
end
end
% 六,设定阈值,将图像二值化
% thresh=1.618*mean2(abs(b)) 可用黄金分割的比例选阈值优点是边缘清晰
e=repmat(logical(uint8(0)),m,n); %创建数组
e(find(b>thresh))=1; %阈值判断二值化
PicOut=e; %函数输出
figure,subplot(1,2,1),imshow(PicInput); %显示原图片
title('原图像');
subplot(1,2,2),imshow(e); %显示拉普拉斯边缘检测后的图片
title('自编函数边缘检测后的图像');
%----------------END OF CODE ----------------function open0207(I,thresh,element)
% 本程序能够对灰度图像先进行二值化,再进行开操作
% 本程序先调用腐蚀函数,再调用膨胀函数,实现开操作
% 作者: archiless lorder
% 一,调用腐蚀函数
[C,B]=erode0207simple(I,thresh,element);
% 二,调用膨胀函数
F=dilate0207simple(C,1,element);
% 三,输出图像
figure,subplot(221),imshow(I),title('原图像');
subplot(222),imshow(B),title('二值化后的图像');
subplot(223),imshow(F),title('开操作后的图像');function close0207(I,thresh,element)
% 本程序能够对灰度图像先进行二值化,再进行闭操作
% 本程序先调用膨胀函数,再调用腐蚀函数,实现闭操作
% 作者: archiless lorder
% 一,调用膨胀函数
[F,E]=dilate0207simple(I,thresh,element);
% 二,调用腐蚀函数
C=erode0207simple(F,1,element);
% 三,输出图像
figure,subplot(221),imshow(I),title('原图像');
subplot(222),imshow(E),title('二值化后的图像');
subplot(223),imshow(C),title('闭操作后的图像');1. 周期函数与线性-周期函数
观察:
clf, x=linspace(0,8*pi,100);
F=inline('sin(x+cos(x+sin(x)))');
y1=sin(x+cos(x+sin(x))); y2=0.2*x+sin(x+cos(x+sin(x)));
plot(x,y1,'k:',x,y2,'k-') legend('sin(x+cos(x+sin(x))','0.2x+sin(x+cos(x+sin(x)))',2)2. plot指令:绘制直角坐标的二维曲线
3. 图形的属性设置和屏幕控制
h=plot(\[0:0.1:2\*pi\],sin(\[0:0.1:2\*pi\])); grid on
set(h,'LineWidth',5,'color','red'); set(gca,'GridLineStyle','-','fontsize',16)设置y坐标的刻度并加以说明,并改变字体的大小。
h=plot(\[0:0.1:2\*pi\],sin(\[0:0.1:2\*pi\]));grid on,
set(gca,'ytick',\[-1 -0.5 0 0.5 1\]), set(gca,'yticklabel','a|b|c|d|e'),
set(gca,'fontsize',20)4. 文字标注指令
plot(x,y1,'b',x,y2,'k-') ,
set(gca,'fontsize',15,'fontname','times New Roman'), %设置轴对象的字体为times New Roman,字体的大小为15
title(' \it{Peroid and linear peroid function}');
%加标题,注意文字用单引号' '加上斜杠'\'后可输入不同的设置,例如it{…}表示花括号里的文字为斜体;如果有多项设置,则可用\…\…\…连续输入。
xlabel('x from 0 to 8*pi it{t}\'); ylabel('\it{y}'); %说明坐标轴
text(x(49),y1(50)-0.4,'\fontsize{15}\bullet\leftarrowThe period function {\itf(x)}');
%在坐标(x(49),y1(50)-0.4)处作文字说明, 各项设置用"\"隔开。
%\fontsize{15}\bullet\leftarrow的意义依次是:\字体大小=15 \ 画圆点 \左箭头
text(x(14),y2(50)+1,'\fontsize{15}The linear period function {\itg(x)}\rightarrow\bullet') %与上一语句类似,用右箭头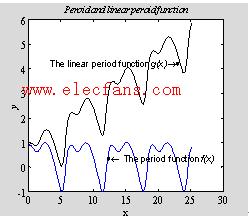
图1 文字标注
观察指令legend和num2str的用法:在同一张图上画出,这里, 并进行适当的标注。
zxy2_2.m
clf, t=0:0.1:3\*pi;alpha=0:0.1:3\*pi;
plot(t,sin(t),'r-');hold on; plot(alpha,3\*exp(-0.5\*alpha),'k:');
set(gca,'fontsize',15,'fontname','times New Roman'),
xlabel('\it{t(deg)}');ylabel('\it{magnitude}');
title(' \it{sine wave and {\it{Ae}}^{-\alpha{\itt}}wave}'); %注意\alpha的意义
text(6,sin(6),'\fontsize{15}The Value \it{sin(t)} at {\itt}=6\rightarrow\bullet', 'HorizontalAlignment','right'),
%上面的语句是一整行,如果要写成两行,必须使用续行号 … ,例如要在“ bullet',”
%后换行,需写“bullet', …”后才能换行。
% 'HorizontalAlignment','right' 表示箭头所指的曲线对象在 文字的右边。
text(2,3*exp(-0.5\*2),['\fontsize{15}\bullet\leftarrow The Value of \it{3e}^{-0.5 \it{t}}=',num2str(3*exp(-0.5*2)),' at \it{t} =2 ']);
%num2str的用法:['string1',num2str,'string2'],注意方括号的使用。
%legend('\itsin(t)','{\itAe}^{-\alphat}') % 请结合图形观察此命令的使用5. 图形窗口的创建和分割
观察:
clf,b=2*pi;x=linspace(0,b,50);
for k =1:9
y=sin(k*x);
subplot(3,3,k),plot(x,y),axis([0,2*pi,-1,1])
end本节通过高等数学的几个例子观察Matlab的三维绘图功能和技巧。
1. 绘制二元函数
◆ 观察:绘制的图象,作定义域的裁剪。
◆ (1) 观察meshgrid指令的效果。
a=-0.98;b=0.98;c=-1;d=1;n=10;
x=linspace(a,b,n); y=linspace(c,d,n);
[X,Y]=meshgrid(x,y);
plot(X,Y,'+')◆ 三维绘图指令mesh、meshc、surf。
◆ (2) 做函数的定义域裁剪,观察上述三维绘图指令的效果。
程序zxy2_4.m
clear,clf,
a=-1;b=1;c=-15;d=15;n=20;eps1=0.01;
x=linspace(a,b,n);y=linspace(c,d,n);
[X,Y]=meshgrid(x,y);
for i=1:n %计算函数值z ,并作定义域裁剪
for j=1:n
if (1-X(i,j))<eps1|X(i,j)-Y(i,j)<eps1 %if语句这样用
z(i,j)=NaN; %作定义域裁剪,定义域以外的函数值为NaN
else
z(i,j)=1000*sqrt(1-X(i,j))^-1.*log(X(i,j)-Y(i,j));
end
end
end
zz=-20*ones(1,n);plot3(x,x,zz),grid off,hold on %画定义域的边界线
mesh(X,Y,z) %绘图,读者可用meshz, surf, meshc在此替换之
xlabel('x'),ylabel('y'),zlabel('z'), box on %把三维图形封闭在箱体里运行了zxy2_4.m 以后,有关向量存储在工作空间中,在此基础上,观察上述等值线绘制指令的运行效果。
[cs,h]=contour(X,Y,z,15); clabel(cs,h,'labelspacing',244)2. 三元函数可视化: slice指令
◆ 观察:绘制三元函数 的可视化图形。
clf,x=linspace(-2,2,40); y=x; z=x;
[X,Y,Z]=meshgrid(x,y,z); w=X.^2+Y.^2+Z.^2;
slice(X,Y,Z,w,[-1,0,1],[-1,0,1],[-1,0,1]),colorbar3. 空间曲线及其运动方向的表现:plot3和quiver指令
clf, t=0:0.1:1.5;
Vx=2*t;Vy=2*t.^2;Vz=6*t.^3-t.^2;
x=t.^2;y=(2/3)*t.^3;z=(6/4)*t.^4-(1/3)*t.^3; %由速度得到曲线
plot3(x,y,z,'r.-'),hold on %画飞行轨迹
%算数值梯度,也就是重新计算数值速度矢量,这只是为了编程的方便,不是必须的
Vx=gradient(x);Vy=gradient(y);Vz=gradient(z);
quiver3(x,y,z,Vx,Vy,Vz),grid on %画速度矢量图
xlabel('x'),ylabel('y'),zlabel('z')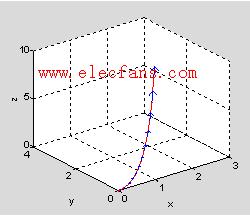
图2 飞机的飞行轨迹与方向
zxy2_3_f.m
function f=zxy2_3_f(x)
f=sin(x+cos(x));zxy2_3.m
clear,clf
a=-8;b=12;n=300;xx=linspace(a,b,n);
h=zxy2_3_f(xx);
S(1)=0;
for i=2:n
S(i)=S(i-1)+quad('zxy2_3_f',xx(i-1),xx(i));
end
subplot(1,2,1),plot(xx,S,'k-'),axis([a,b,-1.5,9])
subplot(1,2,2),plot(xx,[h;zeros(1,length(xx))],'k-'),axis([a,b,-1.5,1.5])◆ 用平行截面法讨论由曲面构成的马鞍面形状。
zxy2_6.m (平行截割法示例,本程序的绘制两曲面交线方法可以套用)
clf, a=-20;eps0=1;
[x,y]=meshgrid(-10:0.2:10); %生成平面网格
v=[-10 10 -10 10 -100 100]; %设定空间坐标系的范围
colormap(gray) %将当前的颜色设置为灰色
z1=(x.^2-2*y.^2)+eps; %计算马鞍面函数z1=z1(x,y)
z2=a*ones(size(x)); %计算平面 z2=z2(x,y)
r0=abs(z1-z2)<=eps0;
%计算一个和z1同维的函数r0,当abs(z1-z2)<=eps时r0 =1;当abs(z1-z2)>eps0时,r0 =0。
%可用mesh(x,y,r0)语句观察它的图形,体会它的作用,该方法可以套用。
zz=r0.*z2;xx=r0.*x;yy=r0.*y; %计算截割的双曲线及其对应的坐标
subplot(2,2,2), %在第2图形窗口绘制双曲线
h1=plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'+');
set(h1,'markersize',2),hold on,axis(v),grid on
subplot(2,2,1), %在第一图形窗口绘制马鞍面和平面
mesh(x,y,z1);grid,hold on;mesh(x,y,z2);
h2=plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'.'); %画出二者的交线
set(h2,'markersize',6),hold on,axis(v),
for i=1:5 %以下程序和上面是类似的,通过循环绘制一系列的平面去截割马鞍面
a=70-i*30; %在这里改变截割平面
z2=a*ones(size(x)); r0=abs(z1-z2)<=1; zz=r0.*z2;yy=r0.*y;xx=r0.*x;
subplot(2,2,3),
mesh(x,y,z1);grid,hold on;mesh(x,y,z2);hidden off
h2=plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'.'); axis(v),grid
subplot(2,2,4),
h4=plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'o');
set(h4,'markersize',2),hold on,axis(v),grid on
end◆ 绘制微分方程 的斜率场,并将解曲线画在图中,观察斜率场和解曲线的关系。
zxy2_5.m (绘制一阶微分方程的斜率场和解曲线)
clf,clear %清除当前所有图形窗口的图像,清除当前工作空间的内存变量。
a=0;b=4;c=0;d=4;n=15;
[X,Y]=meshgrid(linspace(a,b,n),linspace(c,d,n)); %生成区域中的网格。
z=X.*Y; %计算斜率函数。
Fx=cos(atan(X.*Y));Fy=sqrt(1-Fx.^2); %计算切线斜率矢量。
quiver(X,Y,Fx,Fy,0.5),hold on,axis([a,b,c,d])
%在每一网格点画出相应的斜率矢量,0.5是控制矢量大小的控制参数,可以调整。
[x,y]=ode45('zxy2_5f',[0,4],0.4); %求解微分方程。
%zxy2_5f.m是方程相应函数f(x,y)的程序,单独编制;[x0,xs]=[0,4]为求解区间;
%y0=0.4为初始值;输出变量x,y分别为解轨线自变量和因变量数组。
plot(x,y,'r.-') %画解轨线zxy2_5f.m (微分方程的函数子程序)
function dy=zxy2_5f(x,y)
dy=x.*y;1. 地球表面的气温分布(sphere指令)
[a,b,c]=sphere(40);t=max(max(abs(c)))-abs(c);surf(a,b,c,t);
axis('equal'),colormap('hot'), shading flat,colorbar2. 旋转曲面的生成:柱面指令cylinder和光照控制指令surfl
x=0:0.1:10;z=x;y=1./(x.^3-2.*x+4);
[u,v,w]=cylinder(y);surfl(u,v,w,[45,45]);
shading interp3. 若干特殊图形
◆ 运行下面程序,了解各指令的用法和效果。
x=[1:10]; y=[5 6 3 4 8 1 10 3 5 6];
subplot(2,3,1),bar(x,y),axis([1 10 1 11])
subplot(2,3,2),hist(y,x),axis([1 10 1 4])
subplot(2,3,3),stem(x,y,'k'),axis([1 10 1 11])
subplot(2,3,4),stairs(x,y,'k'),axis([1 10 1 11])
subplot(2,3,5), x = [1 3 0.5 5];explode = [0 0 0 1];pie(x,explode)
subplot(2,3,6),z=0:0.1:100; x=sin(z);y=cos(z).*10;
comet3(x,y,z)